In our next topics we have tackle we continue through the application of electric circuit through diagrams and identification of the elements of a circuit. In topic we will discuss the properties relating to the placement of elements in the network and the geometric configuration of the network. these examples are nodes, branch and loops.
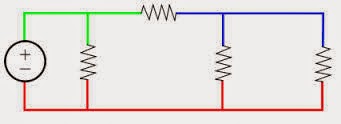
A BRANCH represents a single element such as a voltage source or a resistor
a branch repreents any two terminal element.
In this example branches are represent a single elements, so the branches are
V1 and V2 sources, and R1,R2,R3,R4,R5,R6 restistors are branches.
A NODE is the point of connection between two or more branches.
a node is identified by a dot in a circuit. If a short circuit connects two nodes, the two nodes constitutes a single node.
In the example, the nodes have color indicator, the green, blue , red. the ground is also considered as a node because it is connected to the circuit.
A LOOP is any closed path in a circuit
A loop is a closed path formed by starting at a node, passing through a set of nodes, and returning to the starting node without passing through any node more than once.
Kirchhoff Laws
There are two Kirchhoff laws the KVL and KCL, which kirchhoffs volatage and current law.
-kirchhoff current law states that the algebraic sum of the currents entering a node is zero
as Sir jay taught as, The current entering a node is equal to the current leaving
current leaving=current entering
here how to solve kcl
i1+(-i2)+i3+i4+(-i5)=0
i1+i3+i4=i2+i5
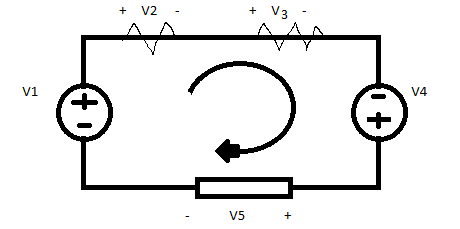
Kirchhoff Voltage Law
KVL is based on the principle of the conservation of energy
Kirchhoff's voltage law states that the algebraic sum of all voltages around a closed path is zero.
here's how to solve KVL
We can start with the voltage source and go clockwise around the loop as shown; then voltages would be -v+v2+v3,-v4, and +v5, in that order. If we reach branch 3, the positive terminal is met first; hence, we have +v3. For Branch , we reach the negative terminal; hence -v4, thus, KVL yields.
-v1+v2+v3-4+v5=0
v2+v3+v5=v1+v4
it is interpreted as :
Sum of Voltage drops = Sum of voltage rises.
Reflection:
As for now im still trying hard to identify how many nodes are in a circuits in times of complicated circuits. And the one cant also understand is by deriving a dependent source which the equation can be more tricky and confusing. As for now we will have our quiz and i hope i can answer that sir jay will give to us. because last meeting he gave as a seat work and its kinda confusing because the resistors and sources have no description given, and so when sir jay answers the seat work. it's not really hard to answer, its just that it was a trick when you loop a kvl or a kcl.



No comments:
Post a Comment