NODAL ANALYSIS 

In this topic we will tackle about nodal analysis ..

Nodal Analysis provides a general procedure for analyzing circuits using node voltage as the circuits variables. Choosing node voltages instead of voltage elements as circuit variables is convenient and reduces the number of equations one must solve simultaneously.
To simplify matters, we shall assume in this section that circuits do not contain voltage sources. Circuits that contain voltage sources will be analyzed in the next section.
In nodal analysis, we are interested in finding the node voltages given a circuit with n nodes without voltage sources, the nodal analysis of the circuit involves taking the following three steps.

Step to Determine Node Voltages:
1. Select a node as the reference node or a ground. Assign voltages v1, v2, ... Vn -1 to the remaining n-1 nodes. The voltages are referenced with respect to the reference node.

2 Apply KCL to each of the n-1 non reference nodes. Use Ohms law to express the branch currents in terms of node voltages.

For example, for the node to the right KCL yields the equation:
Ia + Ib + Ic = 0


Express the current in each branch in terms of the nodal voltages at each end of the branch using Ohm's Law (I = V / R). Here are some examples:



The current downward out of node 1 depends on the voltage difference V1 - V3 and the resistance in the branch.





In this case the voltage difference across the resistance is V1 - V2 minus the voltage across the voltage source. Thus the downward current is as shown.






In this case the voltage difference across the resistance must be 100 volts greater than the difference V1 - V2. Thus the downward current is as shown.




The result, after simplification, is a system of m linear equations in the m unknown nodal voltages (where m is one less than the number of nodes; m = n - 1). The equations are of this form:

where G₁₁, G₁₂, . . . , G_mm and I₁, I₂, . . . , I_m are constants.


NODAL ANALYSIS WITH VOLTAGE SOURCES

Case !

If a voltage souve is connected between the reference node and a nonreference node, we simply set the voltage at the non reference node equal to the voltage of the voltage source. In fig. 3.7 for example 

V1=10v

Thus our analysis is somewhat simplified by this knowledge of the voltage at this node.

Case 1

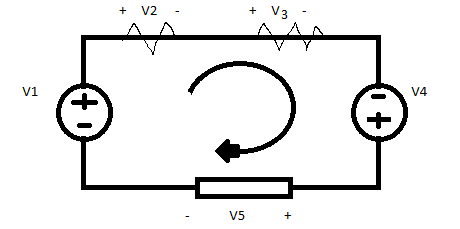
If the voltage source( dependent of independent ) is connected between two nonreference nodes, the two nonreference nodes form generalized node or supernode, we apply both KCL and KVL to determine the node voltages.

A supernode is formed by enclosing a (dependent or independent) voltage source connected between two nonreference nodes and any elements connected in parallel with it.

In Fig. 3.7, nodes 2 and 3 form a supernode. (We could have more than two nodes forming a single supernode. For example, see the circuit in Fig. 3.14.) We analyze a circuit with supernodes using the same three steps mentioned in the previous section except that the supernodes are treated differently. Why? Because an essential component of nodal analysis is applying KCL, which requires knowing the current through each element. There is no way of knowing the current through a voltage source in advance. However, KCL must be satisfied at a supernode like any other node. Hence, at the supernode in Fig. 3.7,

i1 + i4 = i2 + i3                                                                                   (3.11a)
or
v1 − v2 / 2 + v1 − v3  /4 = v2 − 0 / 8 + v3 − 0 / 6                              (3.11b)

To apply Kirchhoff’s voltage law to the supernode in Fig. 3.7, we redraw the circuit as shown in Fig. 3.8. Going around the loop in the clockwise direction gives

−v2 + 5 + v3 = 0 ⇒ v2 − v3 = 5                                                          (3.12)

Note the following properties of a supernode:

1. The voltage source inside the supernode provides a constraint equation needed to solve for the node voltages.

2. A supernode has no voltage of its own.

3. A supernode requires the application of both KCL and KVL.

SERIES PARALLEL CIRCUIT

In this section we will tackle about the series parallel circuit. This topic is also discussed by our teacher when we take up Physics 2. So we in circuits 1 this topic is really applied especially when we find the voltage,current, and resistance. 

SERIES CIRCUIT

A series circuit in which the resistor is connected or short, so the current has only one path. The current flowing through the resistors. The total resistance of the circuit is found by adding up the resistance value of the resistor. 

R=R1+R2+R3+.....

        

   In this example the circuit is a closed path, so the current will flow in counter clockwise, and according to the series resistance, we should total or add the resistances in the circuit

Req=R1+R2+R3

Parallel Circuits:

        A parallel circuit is a circuit in which the resistors are arranged with their heads connected together, and their tails connected together. The current in a parallel circuit breaks up, with some flowing along each parallel branch and re-combining when the branches meet again. The voltage across each resistor in parallel is the same. 
The total resistance of a set of resistors in parallel is found by adding up the reciprocals of the resistance values, and then taking the reciprocal of the total: 
equivalent resistance of resistors in parallel: 
1 / R = 1 / R1 + 1 / R2 + 1 / R3 +... 


Example:

1/Req=R1//R2//R3

=1/10+1/2+1/1

=625ohms

   Resistors are said to be connected in Series, when they are daisy chained together in a single line. Since all the current flowing through the first resistor has no other way to go it must also pass through the second resistor and the third and so on. Then, resistors in series have a Common Current flowing through them as the current that flows through one resistor must also flow through the others as it can only take one path.


   Resistors are said to be connected in Series, when they are daisy chained together in a single line. Since all the current flowing through the first resistor has no other way to go it must also pass through the second resistor and the third and so on. Then, resistors in series have a Common Current flowing through them as the current that flows through one resistor must also flow through the others as it can only take one path.

HOW TO USE THE BREADOARD

Picture of How to use a breadboard

A breadboard also known as protoboard is a type of solderless electronic circuit building.You can build a electronic circuit on a breadboard without any soldering  Best of all it is reusable. It was designed by Ronald J Portugal of EI Instruments Inc. in 1971.

Building or prototyping circuits on a breadboard is also known as 'breadboarding '.

There are various types of breadboard.Breadboard can be found in various sizes and functions.Early amateur radio hobbists used cutting board for bread to prototype there radios thus the name breadboard came.
Some breadboards got built-in powersupply,some got power supply rail and some got only the prototyping section.

A bread board is an array of conductive metal clips encased in a box made of white ABS plastic, where each clip is insulated with another clips. There are a number of holes on the plastic box, arranged in a particular fashion. A typical bread board layout consists of two types of region also called strips. Bus strips and socket strips. Bus strips are usually used to provide power supply to the circuit. It consists of two columns, one for power voltage and other for ground.

NODES,BRANCHES & LOOPS

In our next topics we have tackle we continue through the application of electric circuit through diagrams and identification of the elements of a circuit. In topic we will discuss the properties relating to the placement of elements in the network and the geometric configuration of the network. these examples are nodes, branch and loops.

A BRANCH represents a single element such as a voltage source or a resistor 

a branch repreents any two terminal element.

In this example branches are represent a single elements, so the branches are 

V1 and V2 sources, and R1,R2,R3,R4,R5,R6 restistors are branches.

A NODE is the point of connection between two or more branches.

a node is identified by a dot in a circuit. If a short circuit connects two nodes, the two nodes constitutes a single node.

In the example, the nodes have color indicator, the green, blue , red. the ground is also considered as a node because it is connected to the circuit.

A LOOP is any closed path in a circuit 

A loop is a closed path formed by starting at a node, passing through a set of nodes, and returning to the starting node without passing through any node more than once.

Kirchhoff Laws

There are two Kirchhoff laws the KVL and KCL, which kirchhoffs volatage and current law.

-kirchhoff current law states that the algebraic sum of the currents entering a node is zero

as Sir jay taught as, The current entering a node is equal to the current leaving 

current leaving=current entering 

here how to solve kcl 

i1+(-i2)+i3+i4+(-i5)=0

i1+i3+i4=i2+i5

Kirchhoff Voltage Law

KVL is based on the principle of the conservation of energy

Kirchhoff's voltage law states that the algebraic sum of all voltages around a closed path is zero.

here's how to solve KVL

We can start with the voltage source and go clockwise around the loop as shown; then voltages would be -v+v2+v3,-v4, and +v5, in that order. If we reach branch 3, the positive terminal is met first; hence, we have +v3. For Branch , we reach the negative terminal; hence -v4, thus, KVL yields.

-v1+v2+v3-4+v5=0

v2+v3+v5=v1+v4

it is interpreted as :

Sum of Voltage drops = Sum of voltage rises.

Reflection:

As for now im still trying hard to identify how many nodes are in a circuits in times of complicated circuits. And the one cant also understand is by deriving a dependent source which the equation can be more tricky and confusing. As for now we will have our quiz and i hope i can answer that sir jay will give to us. because last meeting he gave as a seat work and its kinda confusing because the resistors and sources have no description given, and so when sir jay answers the seat work. it's not really hard to answer, its just that it was a trick when you loop a kvl or a kcl.