Super Position Theorem
Super Position Theorem
The Superposition Theorem states that in a linear circuit with several sources, the current and voltage for any element in the circuit is the sum of the currents and voltages produced by each source acting independently. The theorem is valid for any linear circuit. The best way to use superposition with AC circuits is to calculate the complex effective or peak value of the contribution of each source applied one at a time, and then to add the complex values. This is much easier than using superposition with time functions, where one has to add the individual time functions.
Steps in Solving Super Position Theorem
- To calculate the contribution of each source independently, all the other sources must be removed and replaced without affecting the final result.
- When removing a voltage source, its voltage must be set to zero, which is equivalent to replacing the voltage source with a short circuit.
- When removing a current source, its current must be set to zero, which is equivalent to replacing the current source with an open circuit.
Sample Problems
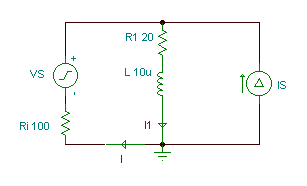
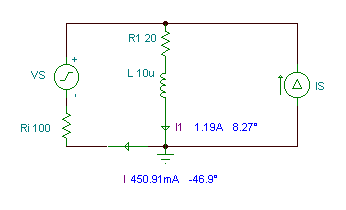
Given:
Ri = 100 ohm, R1 = 20 ohm, R2 = 12 ohm, L = 10 uH, C = 0.3 nF, vS(t)=50cos(wt) V, iS(t)=1cos(wt+30°) A, f=400 kHz.
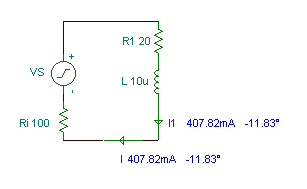
First substitute an open circuit for the current source and calculate the complex phasors I', I1' due to the contribution only from VS.
The currents in this case are equal:
I' = I1' = VS/(Ri + R1 + j*w*L) = 50/(120+j2*p*4*105*10-5) = 0.3992-j0.0836
Next substitute a short-circuit for the voltage source and calculate the complex phasors I'', I1'' due to the contribution only from IS.
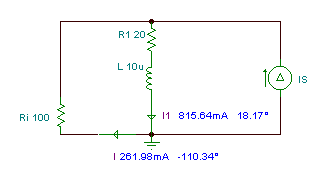
In this case we can use the current division formula:
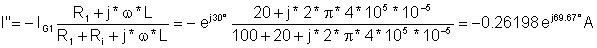
I'' = -0.091 - j 0.246 A
and
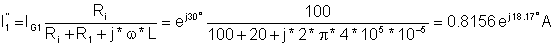
I1" = 0.7749 + j 0.2545 A
The sum of the two steps:
I = I' + I" = 0.3082 - j 0.3286 = 0.451 e- j 46.9° A
I1 = I1" + I1' = 1.174 + j 0.1709 = 1.1865 ej 8.28° A
Note: The final answers for i and i1 are in time domain.
i(t) = 0.451 cos (w×t - 46.9°) A
i1(t) = 1.1865 cos (w×t + 8.3°) A
No comments:
Post a Comment